Zero-Knowledge Proofs: czym są zk-STARK-i i jak działają? (zk-Stark V2)
Czym jest Proof-of-Reserve i Zero Knowledge Proof?
Proof-of-Reserve (PoR)
Jest to sposób dla giełd kryptowalutowych, aby pokazać, że mają wystarczające aktywa, aby pokryć wszystkie salda klientów. To buduje zaufanie, udowadniając, że giełda nie ukrywa żadnych zobowiązań. Najprostszym sposobem na pokazanie tego jest opublikowanie zarówno kwot aktywów giełdy, jak i listy sald użytkowników, aby każdy mógł to potwierdzić:
Całkowita wartość aktywów użytkowników, które OKX twierdzi, że posiada, to suma całkowitego salda aktywów każdego użytkownika.
Całkowite saldo każdego użytkownika jest większe niż zero, a ich aktywa są uwzględnione, pokrywając ich zobowiązania i zapewniając, że każdy użytkownik ma dodatnią wartość netto.
Giełda deklaruje całkowitą wartość dla każdego pojedynczego użytkownika, więc każdy użytkownik powinien mieć możliwość zweryfikowania włączenia swojej wartości netto do wartości całkowitej
Jednak ujawnienie tych sald może zagrozić prywatności użytkownika. Aby to rozwiązać, używamy metody zwanej Zero Knowledge Proof (ZKP), aby chronić prywatność użytkownika.
Zero Knowledge Proof (ZKP)
Jest to technika zabezpieczeń, która pozwala giełdzie kryptowalut udowodnić, że dane stwierdzenie jest prawdziwe, nie ujawniając żadnych dodatkowych informacji.
W naszym przypadku chcemy udowodnić, że mamy wystarczające środki, nie dzieląc się szczegółowymi danymi użytkowników. Większość ZKP-ów należy do dwóch kategorii:
zk-SNARK
zk-STARK
Używamy zk-STARK, ponieważ jest bezpieczniejszy i ma minimalne założenie dotyczące bezpieczeństwa. W tym artykule wyjaśnimy, jak używamy zk-STARK, aby chronić prywatność użytkowników, jednocześnie udowadniając naszą wypłacalność.Zanim przejdziemy dalej, pomocne jest zrozumienie kilku podstawowych terminów ZKP, takich jak obieg, drzewo Merkle'a i zobowiązania.
Dostępne jest wiele zasobów dla początkujących, które pomogą im zacząć. Zaawansowani użytkownicy mogą zapoznać się z Kursem MOOC i monografią akademicką.
Jak działa zk-STARK?
Tworzymy drzewo Merkle'a, używając hasha konta każdego użytkownika jako liści. Każde konto pokazuje salda w USD dla różnych tokenów (n.p., BTC, ETH). Aby zarządzać tymi saldami, dzielimy salda na nieujemne kapitały i długi dla każdego tokena. W ten sposób pracujemy tylko z liczbami dodatnimi, co ułatwia przeprowadzanie obliczeń i unikanie błędów.
Na przykład:
Jeśli saldo tokena BTC użytkownika wynosi A, jego kapitał BTC wynosi A, a dług BTC wynosi 0.
Jeśli saldo tokena ETH użytkownika wynosi -B, jego odpowiadający kapitał wynosi 0, a dług wynosi B
Następnie budujemy drzewo Merkle'a z tymi wartościami kont jako liśćmi. Korzeń drzewa działa jako pojedyncza wartość reprezentująca wszystkie salda użytkowników. Każdy użytkownik może udowodnić, że jego konto jest częścią tego drzewa, używając Ścieżki Merkle'a, która pokazuje, jak jego konto łączy się z korzeniem.
Publikujemy również łączny kapitał własny i zadłużenie zsumowane dla wszystkich tokenów i użytkowników. Następnie tworzymy Zero Knowledge Proof (ZKP, po polsku: dowód zerowej wiedzy), aby pokazać dwie rzeczy:
Dowód sumy: wartości kapitału własnego i długu w drzewie Merkle'a sumują się poprawnie
Dowód nieujemności: całkowity kapitał każdego użytkownika jest większy niż ich całkowity dług
Kiedy próbujemy zweryfikować drzewo Merkle'a dla dużej liczby kont, staje się to zbyt trudne do obsłużenia za jednym razem. Aby pokonać to wyzwanie, dzielimy konta na mniejsze grupy zwane partiami. Każda partia jest przetwarzana osobno za pomocą obwodów partii, które sprawdzają dolną część drzewa Merkle'a.
Grupowanie nie tylko sprawia, że jest to wykonalne, ale także pozwala nam przeprowadzać te kontrole jednocześnie (przetwarzanie równoległe). Gdy mamy wyniki z każdej partii, używamy kolejnej warstwy obwodów, zwanej obwodami rekurencyjnymi, aby połączyć i zweryfikować wszystkie partie razem, aż udowodnimy całe drzewo Merkle'a.
Czym jest obwód wsadowy (Batch Circuit)?
Obwód wsadowy bierze pod uwagę 1024 konta (acc0, acc1,..., acc1023) jako dane wejściowe i generuje 3 główne wyjścia: hash (hbatch), całkowitą wartość kapitału (ebatch), oraz całkowitą wartość zadłużenia (dbatch). Sprawdza, że:
Całkowity kapitał własny każdego konta wyrażony w USD jest większy niż jego całkowity dług.
ebatch to suma wszystkich wartości kapitałowych denominowanych w USD na tych kontach
dbatch jest sumą wszystkich wartości zadłużenia denominowanych w USD na tych kontach
hbatch jest korzeniem drzewa Merkle'a utworzonego przy użyciu hashy kont
Nie ma przepełnienia podczas sumowania dla ebatch i dbatch
Co to jest obwód rekurencyjny (Recursive Circuit)?
Obwód rekurencyjny wymaga 64 różnych dowodów (π0, ..., π63), hashe (h0, ..., h63), kapitały (e0, ..., e63) i długi (d0, ..., d63) z dolnych obwodów jako wejścia. Łączy te dane wejściowe i produkuje 3 wyniki: nowy hash (hrekurencyjny), łączny kapitał (erekurencyjny) oraz łączny dług (drekurencyjny). Sprawdza, że:
Każdy z 64 dowodów jest poprawny
Każdy dowód π0, ..., π63 z dolnej warstwy obwodu jest poprawny
erekurencyjny jest sumą e0, ..., e63
drekurencyjny jest sumą d0, ..., d63
hrekurencyjny jest hashem konkatenacji (concatenation) h0, ..., h63, i.e.
hrekurencyjny = Hash (h0 || h1 || ... || h63)
Nie ma przepełnienia podczas sumowania dla erekurencyjny i drekurencyjny
Jaki jest związek między obwodami wsadowymi a obwodami rekurencyjnymi?
Diagram poniżej ilustruje, jak obwód wsadowy i obwody rekurencyjne łączą się i przekazują dane między sobą. Pamiętaj, że w diagramie duplikujemy obwody w celach ilustracyjnych, ale w naszej implementacji używamy tylko jednego obwodu dla każdej warstwy.
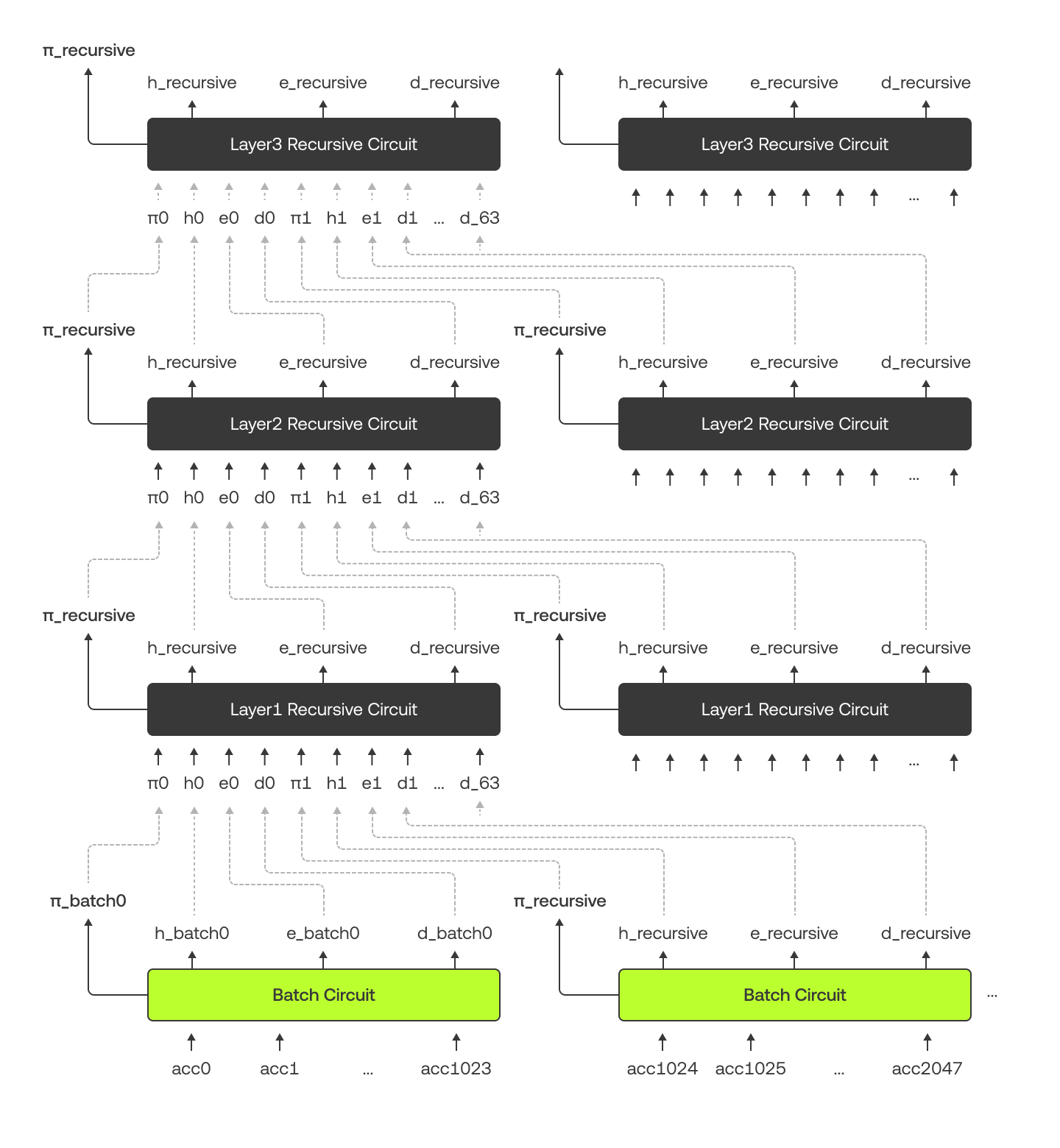
Nasz drzewo Merkle'a jest zbudowane nieco inaczej. Na dolnych 10 poziomach każdy węzeł nadrzędny ma 2 węzły podrzędne, podczas gdy na wyższych poziomach każdy węzeł nadrzędny ma 64 węzły podrzędne. To dlatego, że obwody wsadowe obsługują dolną część, a obwody rekurencyjne zarządzają górną częścią. Diagram poniżej używa przykładu z „Alicją”, aby pokazać drzewo Merkle'a i jej dowód Merkle'a (w kolorze zielonym).
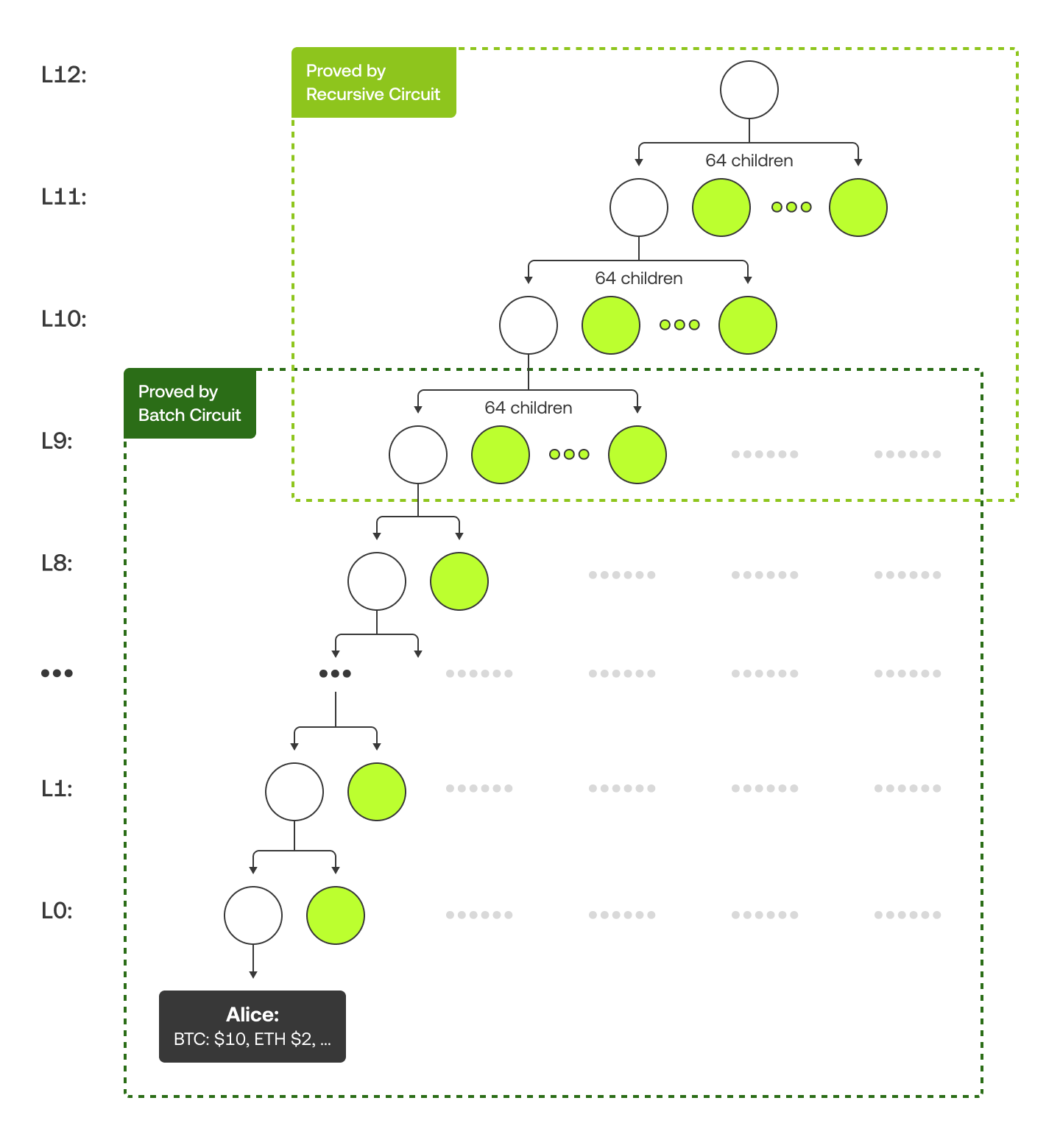
Aby uzyskać więcej szczegółów technicznych, takich jak to, jak dostosowujemy numery kont do rozmiaru partii lub wybieramy odpowiedni algorytm hashujący, zapoznaj się z tą stroną.
Postępy w zk-PoR wersja 2
Nasza wersja 2 zk-PoR poczyniła kilka postępów w porównaniu do poprzedniej wersji:
Większa efektywność: Jest teraz 50 razy szybszy niż poprzednia wersja. Zajmuje to 3 godziny na pojedynczej maszynie 10-rdzeniowej, w porównaniu do 36 godzin w poprzedniej wersji przy użyciu dziewięciu maszyn 64-rdzeniowych. Przyspieszenie to wynika z użycia frameworka Plonky2, który kompiluje obwody napisane w Rust do wydajnego języka maszynowego, zamiast korzystać z wolniejszych skryptów Pythona. Zwiększyliśmy również Plonky2, aby wykonywał obliczenia na GPU, co skróciło czas o dodatkowe 30%.
Lepsza audytowalność: W wersji 2 używamy wysokopoziomowego frameworka, który obsługuje złożone szczegóły kryptograficzne za nas. Dzięki temu nasz kod jest bardziej przejrzysty, czytelny i mniej podatny na błędy.
Zwięzły dowód: Rozmiar dowodu V2 (~500KB) wynosi tylko 0.05% V1 (~1.2GB). Dzięki metodzie rekurencyjnej dowody mogą być wielokrotnie agregowane i kondensowane w jeden dowód.
Jak przeprowadzić samoweryfikację za pomocą opcji Proof of Reserves (PoR)?
Oto jak możesz sprawdzić, czy saldo Twojego aktywa jest uwzględnione jako liść Merkle zk-STARK:
Zaloguj się na swoje konto OKX, przejdź do Aktywa i wybierz raporty PoR
Wybierz Szczegóły, aby wyświetlić dane audytu
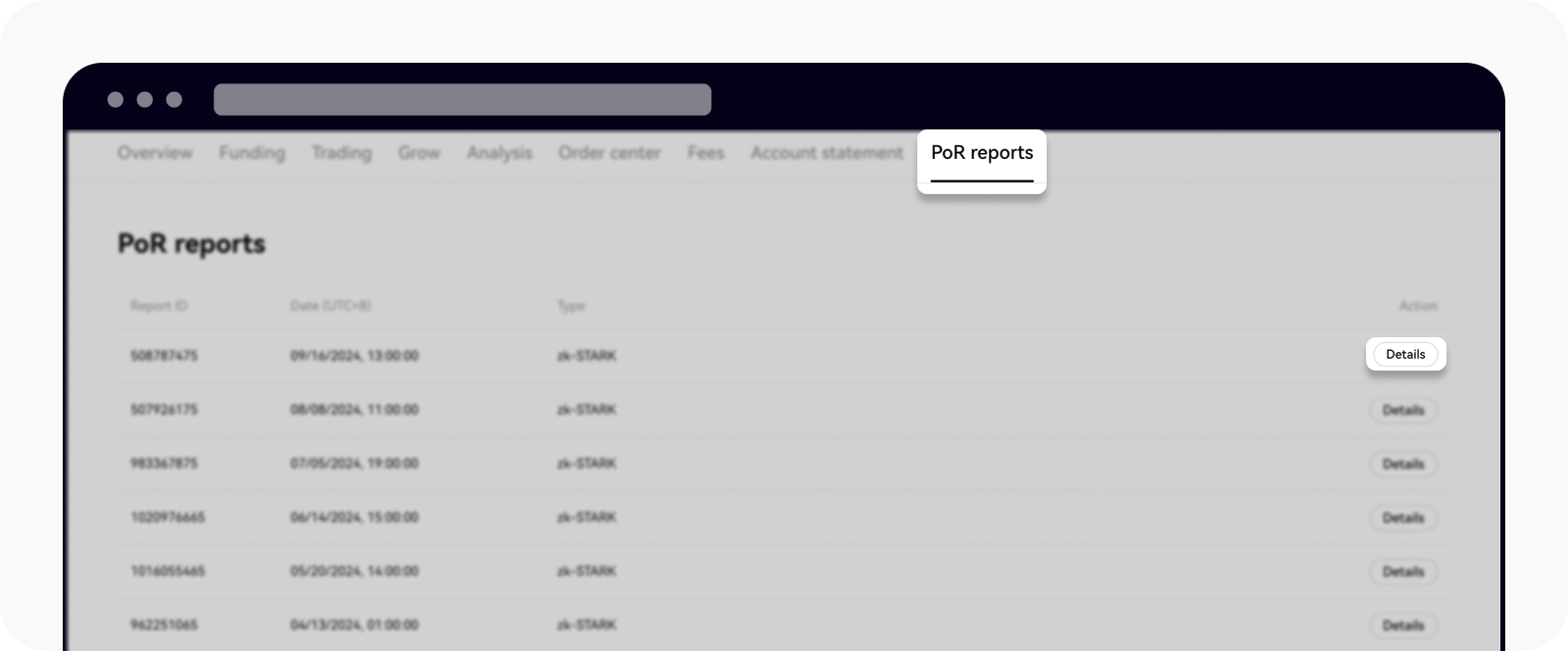
Pobierz dane potrzebne do ręcznej weryfikacji, wybierając opcję Kopiuj dane
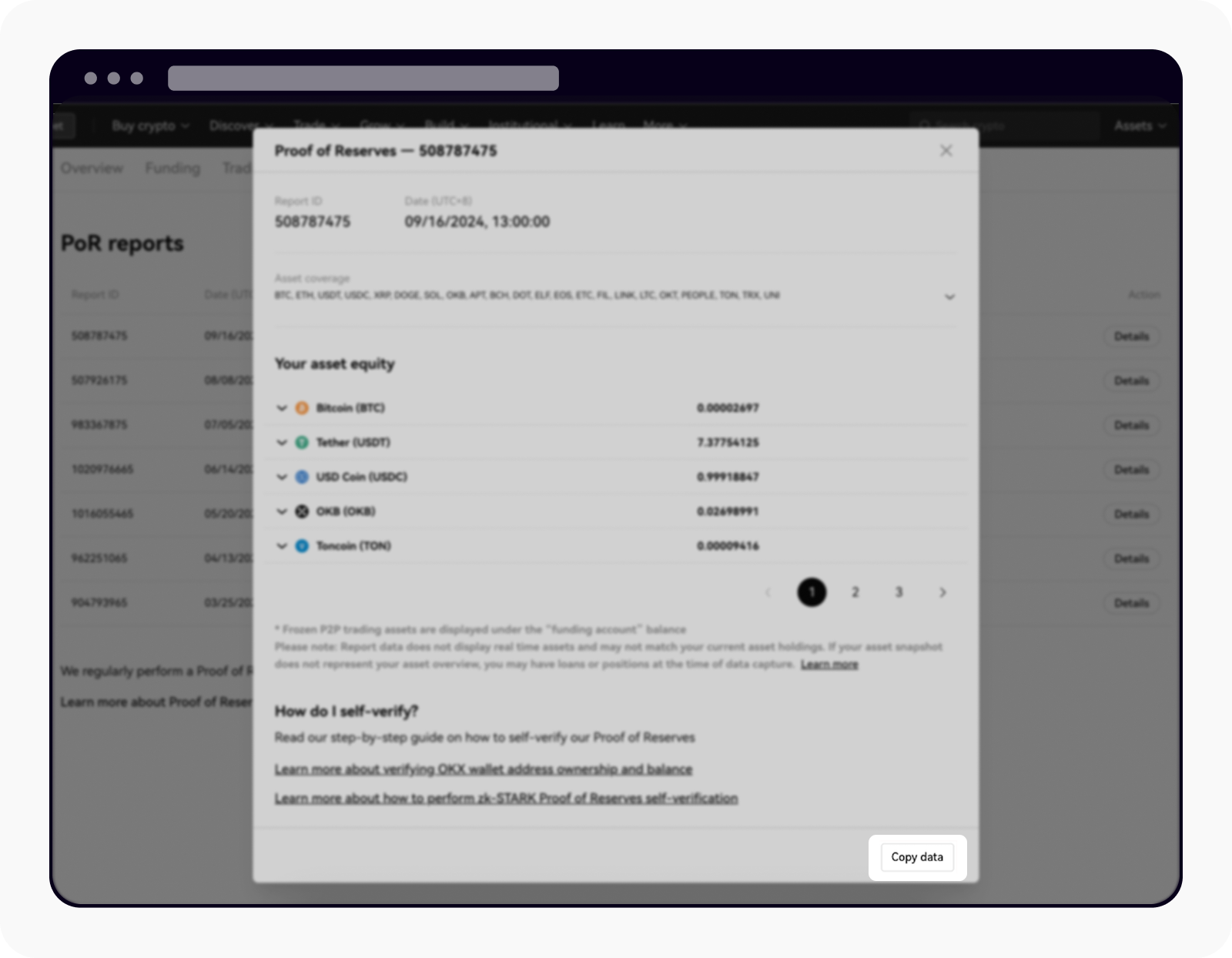
Po wybraniu Kopiuj dane, otwórz edytor tekstowy (n.p. używając notatnika) następnie wklej i zapisz ciąg JSON jako plik. Plik musi kończyć się nazwą "_inclusion_proof.json." Ciąg JSON zawiera saldo konta i odczyt ścieżki Merkle, a następnie zapisuje plik w nowym folderze
Otwórz edytor tekstowy (n.p., Notatnik), a następnie wklej i zapisz ciąg JSON jako plik. Nazwa pliku musi kończyć się na "_inclusion_proof.json." Zapisz plik w nowym folderze
Ciąg JSON zawiera saldo Twojego konta oraz odczyt ścieżki Merkle.
Tekst JSON jest pokazany poniżej:
{"sum_tree_siblings":["9ffb169fecf075e203edca2af65e4c69fa4331d13ac75ccae4cd5b990c91b675","7149661a789763cb61293ebf5d8bdd5570e79ee203738f87a444c79642b89a79","788aac9e392fa62bc3f79c98c7afd7bb41ee7d5bd496876cd0580080f19e002f","e828a44d345e6799e232aabc57cb2b92986ee1c52b65344d83e79d84b4b571b7","6c0675de9cd6b2be1abd6a98260e7ea776492c4aa9aadf31086f23452cb7c48d","2dfe3aadb5ac00ee0b1110ee8c313afdee85d9f9c62904d6ee79c8f02354d80a","5068ae26192587432892a6de8b54ea25a8aafd1c010ab5e67b55b2c30c6257fa","a1bb026ec9f3d8a1fa1b6f498c40ed8b117a57e1af9816d08d9135ab4fe43a60","119dfcd214191405b7f7f7c7091b89196c0cae818bfcd8252a48f20d9cf3c378","4d9403482ca177c669df34a60bb2afab7a18097012d0b70703c8e59258cdfee6"],"recursive_tree_siblings":[{"right_hashes":["e041eaa366259f873e9e1477aac77362f4b1b460c2d5e1c14907fa9288d66cff","b45a8c503e649ff39543a918996b06fc65f4df9b61d071b22f7342f94862c9be","e00ec1225dfe6b7e950f6b9b8e9d1121bf17eb60c444fd7191b861a2ddddad23","c02c12beb73c03f996508cdce7bef927f0aa8b77ebd899f6a75df83de9d4022e","d36b95f14c5fd5bfaf1347e3177340e2fc9475a77b852321b80527132e7d539c","c0b9770178e70a7bba4ac8aeaadab2bcb2ae7f90d0f678bd463f2c42ff4f4a7b","fab5e7c6f7f8bc6d51f515c5db235cc1ebe987adee8c19c9bc7313e9e266d72c","b3884fb88fc95949c78ca8867cfa9e8a3c4c59fa1a48d8371f7fbfbebda0acfd","0c6da9bdbd40065f92ddaa45297670f2f0bffedb74020c5d5752e70d8b507b77","left_hashes":["1101beee3c6a36a168ceee9d43fcf6cb6de7e5c87ed4d22cd0308c9870d17839","d40a8e9eb4c873996ec515600def480eaa9378ca8481a7bcdf5f77725dbec4ae","63b12566ba8473f502386e92d500664cb63683dca6c26593378dcc9715257b77","166440a8ccbfbc1ce6ec5efaf8bc0b25e1bf692fa972e2729e45ce709d1d35a3","724451ad1d937fc47de5ede930d159dce78093d5e6a1f2e698452f8a29b4de3a","081a88f12d4e23173a1bf5038d4a9413cc92dd421c92261065de06492b5010ec","a76dbb1d4c393539b9546f4460d50ebc7582748d7de63c62c463b793c55bac7c","91e6c21de3f4060e1bd864131a570af42de31bbcd84a5afcbbc8fedcbf806002","fad08eca5bfdc5f37d39eabb44c2216afc6498afcb6b913d72586eaaf132a572","d39b06fe28387ba8045e2b2f95e90613916beef4f79df7961514e6e4cbfd07fa","81d07e300a116a0e4fcb56c39715c5fd5921abe8d10329b07c3f33d417b70ca8","7b72a7e62a45c9958a8a55eec2ba47352f2af701bacba098668589f6a3ce0423","8766bc64c38c2bb4188d89de0e732bca103daaed0c779cba9a8b191e24b51c9c","fa57ae4409e46c605f3cbfd01dfd9ccebc86cbd765cdc067206cb9367832442f"]}]}..... "index":9583119,"account":{"id":"50f5f08cc5036e15a541c64ac4ac6d2d9aa8ddab1ec32ed58b10e6ed3edfad59","debt":["0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0"],"equity":["8412384","9386185","45265193","0","0","8751","3824171","2716990","0","313671","28319","0","0","0","41261","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","142353","0","0","0","0","0","4435","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","662","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","993","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","25132","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","305","0","0","0","0","0","0","0","0","6141","0","0","0","0","0","0","0","0","0","0","0","5511","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0"]}}
Pobierz narzędzie weryfikacji OKX typu open-source: zk-STARKValidator
Zapisz narzędzie do weryfikacji typu open-source od OKX, zk-STARKValidator, i plik ciągu JSON razem w nowym folderze wymienionym w kroku 5. W naszym przypadku, zamieszczamy narzędzie oraz plik danych w folderze Pobrane, pod nazwą „proof-of-reserves”, jak pokazano poniżej:

Otwórz zk-STARKValidator, który automatycznie uruchomi plik JSON zapisany w folderze
Sprawdź wynik:
Jeśli weryfikacja będzie pomyślna, pojawi się komunikat Weryfikacja ograniczenia włączenia zakończona pomyślnie (Inclusion constraint validation passed):

Jeśli weryfikacja będzie niepomyślna, pojawi się komunikat Weryfikacja ograniczenia włączenia zakończona niepowodzeniem (Inclusion constraint validation failed):

Jak zweryfikować łączne saldo zk-STARK i ograniczenie nieujemne?
Poniżej przedstawiamy, w jaki sposób można zweryfikować, czy posiadane przez nas aktywa są prawdziwe i czy żaden użytkownik nie posiada ujemnego kapitału netto:
Przejdź do naszej strony Proof of Reserve i wybierz Raport o odpowiedzialności
Pobierz plik zk-STARK i zapisz go w nowym folderze
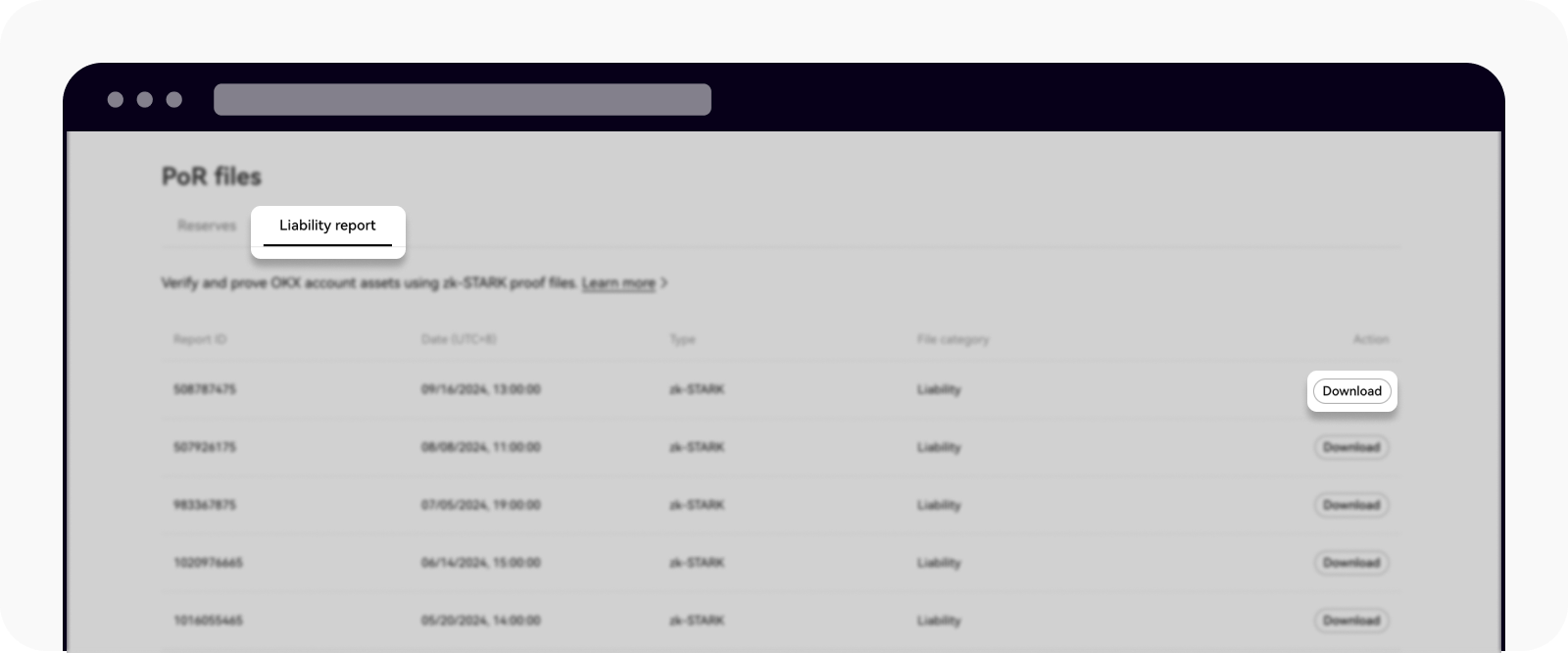
Rozpakuj plik, aby wyodrębnić plik "sum_proof_data.json"

Pobierz narzędzie weryfikacji OKX typu open-source: zk-STARKValidator
Zapisz narzędzie do weryfikacji OKX typu open-source, zk-STARKValidator, oraz plik "sum_proof_data.json" razem w nowym folderze utworzonym w kroku 2. W naszym przypadku, zamieszczamy narzędzie oraz plik danych w folderze Pobrane, pod nazwą „proof-of-reserves”, jak pokazano poniżej:

Otwórz program zk-STARKValidator, który automatycznie uruchomi plik sum proof data zapisany w folderze.
Sprawdź wynik
Jeśli weryfikacja zakończy się pomyślnie, zostanie wyświetlony wynik Walidacja sumy całkowitej i ograniczenia nieujemnego zakończona pomyślnie (Total sum and non-negative constraint validation passed):

Jeśli weryfikacja zakończy się niepowodzeniem, zostanie wyświetlony wynik Walidacja sumy całkowitej i ograniczenia nieujemnego nie została zakończona pomyślnie (Total sum and non-negative constraint validation failed):

Aby zbadać więcej szczegółów technicznych, nasz system Proof of Reserves jest open-source i dostępny do przeglądu i użycia na github.






